[BOJ 1753][백준 1753번] 최단 경로 (파이썬 풀이)
도깨비젤리
·2021. 5. 19. 17:50
https://www.acmicpc.net/problem/1753
1753번: 최단경로
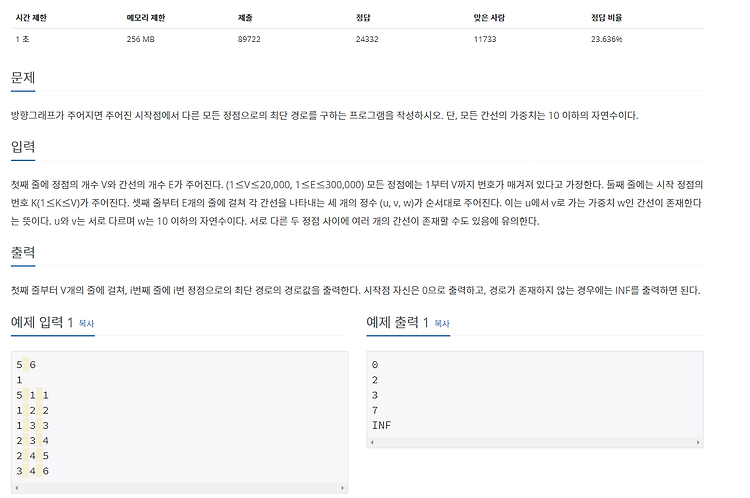
첫째 줄에 정점의 개수 V와 간선의 개수 E가 주어진다. (1≤V≤20,000, 1≤E≤300,000) 모든 정점에는 1부터 V까지 번호가 매겨져 있다고 가정한다. 둘째 줄에는 시작 정점의 번호 K(1≤K≤V)가 주어진다.
www.acmicpc.net
🤔 문제 설명 및 입출력

✍ 접근 방법
1. 그래프를 탐색해야한다.
2. 근데 edge에 (음수가 아닌) 가중치가 붙어있다.
3. 다익스트라 알고리즘으로 푼다!
라는 사고방식이 머리 속 깊이 박혀 있었기 때문에, 다익스트라를 통한 풀이법을 생각하는 것은 어렵지 않습니다.
다만 "이것을 어떻게 최적화 할까?" 라는 물음에 답하는 것이 어려웠지요.
입력값이 1<= V<=20,000 , 1<=E<=300,000 인 시점에서 확실히 뭔가 가지치기를 할 트릭이 필요하겠구나~ 라는 생각이 들긴 들었는데, 참...알잖습니까 생각한대로 구현을 한다는게 마냥 쉬운 일이 아니더라고요
말이 조금 밖으로 샜는데, 문제 풀이를 위해서는 기본적으로 아래와 같은 다익스트라 풀이법을 적용합니다
- 시작 노드로부터 각 노드의 거리를 나타내는 리스트 distance를 생성한다. distance의 각 요소는 엄청나게 큰 수로 초기화 한다.
- 시작 노드를 queue로 삼아, queue가 텅 빌 때까지 (전문용어로 앵꼬) 탐색을 한다.
- 탐색 방법
- 큐에서 튀어나온 이동 가능한 노드(node) / 이동에 드는 비용(dis)을 받는다,
- 현재 노드까지 이동하는데 든 비용(min_dis)와 dis를 더한다.
- 2 에서 더한 값이 distance[node] 보다 작다면 값을 갱신해준다. (최소 거리를 경신했으니 계속 탐색)
- 그렇지 않다면 스킵하고 위 과정을 반복한다
- 탐색 방법
근데 단순히 이렇게만 하면 위에서 말했듯, 시간 복잡도 / 공간 복잡도 측면에서 아웃이 되므로 이를 최적화 하기 위한 장치들을 코드 곳곳에 심어야합니다.
최적화를 위한 장치들
1. 그래프를 인접행렬 꼴이 아닌 인접 리스트 꼴로 만든다
- 인접 행렬로 만들면 공간복잡도가 O(N^2)로 급상승하여 메모리 초과가 납니다.
2. 그래프 탐색을 단순 queue가 아닌, heap을 이용해서 시행합니다.
- 파이썬에는 이미 잘 만들어진 바퀴인 heapq 모듈이 존재합니다.
3. 입력을 받을 적에 input() 이 아닌 sys.stdin.readline()을 이용합니다.
- 입력횟수가 작으면 모를까, 이렇게 어마무시한 입력이 들어올때는 sys.stdin.readline()을 쓰는걸 고려해봅시다.
- 확실히 input() 보다는 빠르게 동작합니다.
4. 방문 여부를 체크하는 visited 리스트를 만들어, 가지치기를 합시다.
- 한번 노드의 탐색이 끝나면, 해당 노드에서 얻을 수 있는 최소거리가 구해지기에 다시 방문할 필요가 없어집니다.
다익스트라 기본 풀이법과 위에 기재된 최적화를 위한 장치들을 코드에 쌈박하게 구현할 방법을 생각하면서 문제를 풀어봅시다.
👨💻 소스 코드
- 파이썬
import sys import heapq # key 1 :시간을 줄이기 위해서 input 보다 더 빠른 입력, readline()을 사용했다 V,E = map(int,sys.stdin.readline().split()) # 정점의 갯수 V , 간선의 개수 E K = int(input()) # 시작 정점의 번호 # key 2 : 인접 행렬로도 그래프를 그릴 수 있는데, 그러면 공간 복잡도가 O(N^2) 이 되어서 메모리 초과가 난다. graph = [[] for _ in range(V+1)] INF = float('inf') # 초기값 셋팅 distance = [INF] * (V+1) # 노드별 거리 초기화 distance[K] = 0 # 시작노드 거리 초기화 # 그래프 그리기 : 어짜피 heapq를 이용하여 거리 순으로 자동 오름차순 정렬 할 것이기 때문에 # 입력 받으면서 출발/도착 노드가 같은 경우의 최소 가중치를 계산하여 넣을 필요가 없다. for _ in range(E): u,v,e = map(int,sys.stdin.readline().split()) graph[u].append((v,e)) # key 3: 방문 체크를 시행하여, 이미 최소값이 나온 노드에 대해서는 다익스트라를 수행하지 않는다 # heapq를 이용하기 때문에 while heap이 끝나는 그 시점에서 해당 노드를 방문하는 최소 거리가 보장된다. visited = [False] * (V+1) heap = [] heapq.heappush(heap,(0,K)) # K번 노드로부터 모험을 떠나므로, 거리가 0인 상태로 시작한다 while heap: min_dis, cur_node = heapq.heappop(heap) # 현재 경로를 탐색할 노드가 이미 방문한 적이 있는 노드라면 스킵한다. if visited[cur_node]: continue # 방문 한 적이 없는 노드라면, 방문 처리를 해준다. visited[cur_node] = True # 현재 노드와 연결된 모든 노드와 거리를 대상으로 이하의 검사를 시행한다. for node,dis in graph[cur_node]: # 1. new_d 는 현재 노드까지 오기 까지의 거리 min_dis와 현재 노드에서 node까지의 거리인 dis의 합이다. new_d = min_dis+dis # 2.만약에 이렇게 계산한 거리가 기 저장되어있었던 거리보다 작다면, 값을 바꿔준 다음, heap에 새로운 값을 투입해준다. # (더 탐색할 가치가 있다는 뜻으로 넣어주는 것이다.) if new_d < distance[node]: distance[node] = new_d heapq.heappush(heap,(new_d,node)) # 문제의 출력 형식에 맞추어 출력 for idx in range(1,len(distance)): if distance[idx] == INF: print('INF') else: print(distance[idx])
🔥 강평
수많은 메모리 초과 / 시간 초과 에러를 극복해서 도출한 정답인만큼 굉장히 기분 좋았습니다.
여태까지 다익스트라 알고리즘을 구현할때는 내가 보기 편하다는 이유로 인접 행렬을 통한 구현을 했는데, 이렇게 빠른 시간이 필요한 문제를 풀어야할 경우를 대비해서 인접 리스트로도 구현하는 방법에도 익숙해져야겠다는 생각을 했습니다.
역시, 알고리즘의 세계에서는 하나만 알아서 오만곳에 다 써먹는 게으른 사고방식으로는 살아남을 수 없는 것 같습니다.
'Algorithm > Baekjoon' 카테고리의 다른 글
| [BOJ 10814][백준 10814번] 나이순 정렬 (파이썬 풀이) (0) | 2021.06.02 |
|---|---|
| [BOJ 1865][백준 1865번] 웜홀 (파이썬 풀이) (0) | 2021.06.02 |
| [BOJ 1149][백준 1149번] RGB거리 (파이썬 풀이) (0) | 2021.06.01 |
| [BOJ 10826][백준 10826번] 피보나치 수 4 (파이썬 풀이) (0) | 2021.05.19 |
| [BOJ 1932][백준 1932번] 정수 삼각형 (파이썬 풀이) (0) | 2021.05.16 |





